Introduction
After a study of an abstract resource allocation game in the two preceeding articles (‘A Three Slots Resource Allocation Study Definitely Not In Marvel Snap‘, ‘Resource Allocation Game With 3 Slots – Numerical Analysis‘), we move into another elementary topic loosely related to Marvel Snap. Nevertheless, the question we would ask here is vital for the real game: ‘what conditions have to be satisfied for Player 1 to win against Player 2 in the very last move?’
We would restrict ourselves only to pure point effects.
How a game of Marvel Snap is won?
To achieve the victory in a game of Marvel Snap, Player 1 (P1) has to win on at least one location more than P2, or in case of a tie, have more points in total. Winning a location means having more points than opponent on it.
Consequently, not the absolute number of points is the crucial variable for the final success, but the relative power with respect to opponent on each location. A basic game of Snap consists of 6 rounds in which players could react to board state. Assuming that both sides have similar total number of points to allocate, the objective becomes to win two locations with least possible investment (smallest point difference). What should especially be avoided is commiting too much resources into a location where opponent gave up. Let’s introduce some notation for the rest of the article.
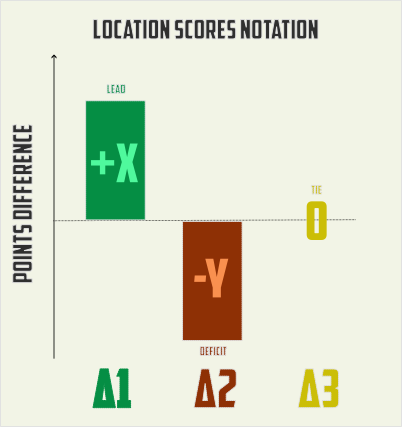
The symbols Δ1, Δ2, Δ3 refer to point difference on 1,2,3 locations. A board state could be written as (-2,+4, 0) for example, where Δ1=-2 and so on.
We would restrict ourselves only to pure points (in real game cards like Hulk, Cyclops…), neglect any board clogging issues etc., therefore all board states could be ordered from biggest ‘+’ to lowest ‘-‘ with no lose of information. This way duplicate rolls are removed. So in our example (-2,+4,0) => (+4,0,-2).
Duel Of Chonkers And Point Reach
Let’s dive into the first, simplest case study. Both sides would play just one finisher card in the last turn, contributing points to only one row (e.g. two Hulks). What board state favors P1?
Obviously, P1 wins everytime if leading on all locations before ‘Hulks’ get deployed. Such scenario is highly unlikely though given that both sides have access to similar resources.
The real point of interest is P1 winning on two locations. Let’s take the simplest spread of this kind: (+N, +N, -2N). If ‘Hulk’ power is greater than 2N, then P1 is guaranteed to win by placing him on the 3rd slot and taking a small lead there.
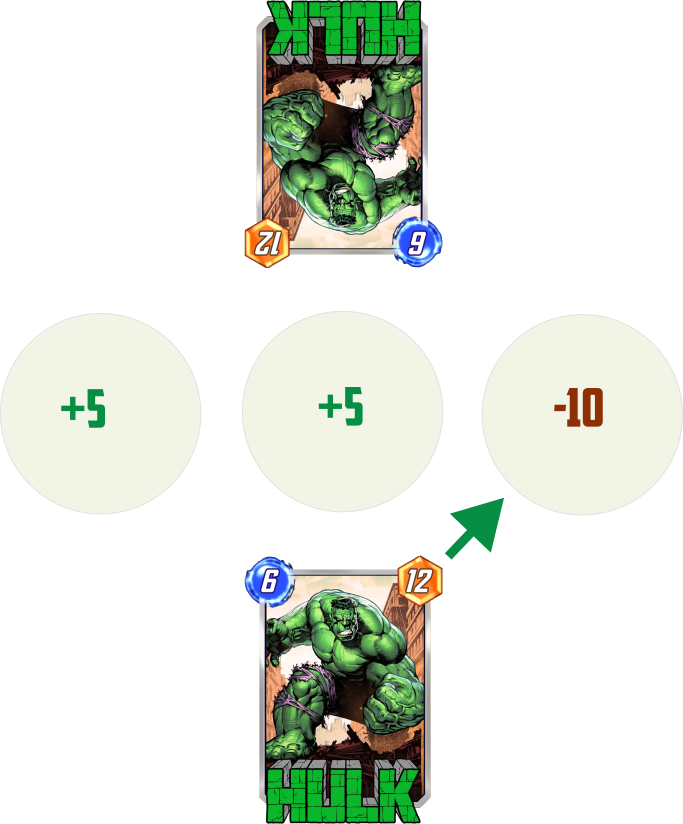
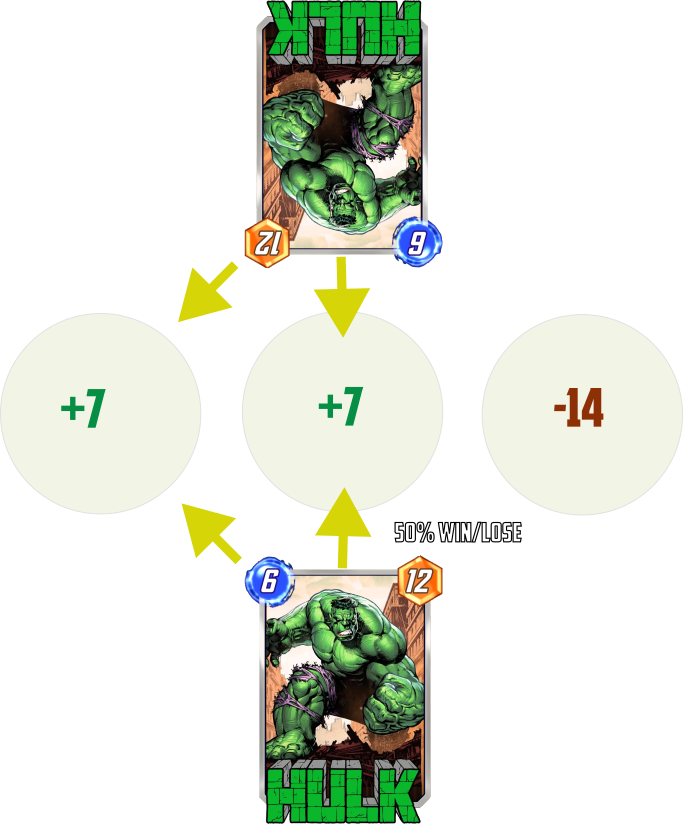
If ‘Hulk’ power is smaller than this gap, then P1 doesn’t have a way to get ahead on 3rd slot and have to choose between 1st and 2nd. P2 would aim for same slots. If Hulks go into the same lane, then P1 wins, if to different, then P2 wins. In spite of the initial lead, there is only 50% for P1 to claim victory after last turn and everything comes down to a coinflip.
Let’s visualize it once more. If the ‘Hulk’ is indeed a Hulk with 12 body, then gap of 13 points is enough to secure third location for P2 => 50% P1 winrate. Gap of 11 or less => 100% P1 winrate. We said that both players should avoid overinvestment, but now it suddenly appears that there exist a reach threshold, crossing which leads to a clear and impactful benefit.
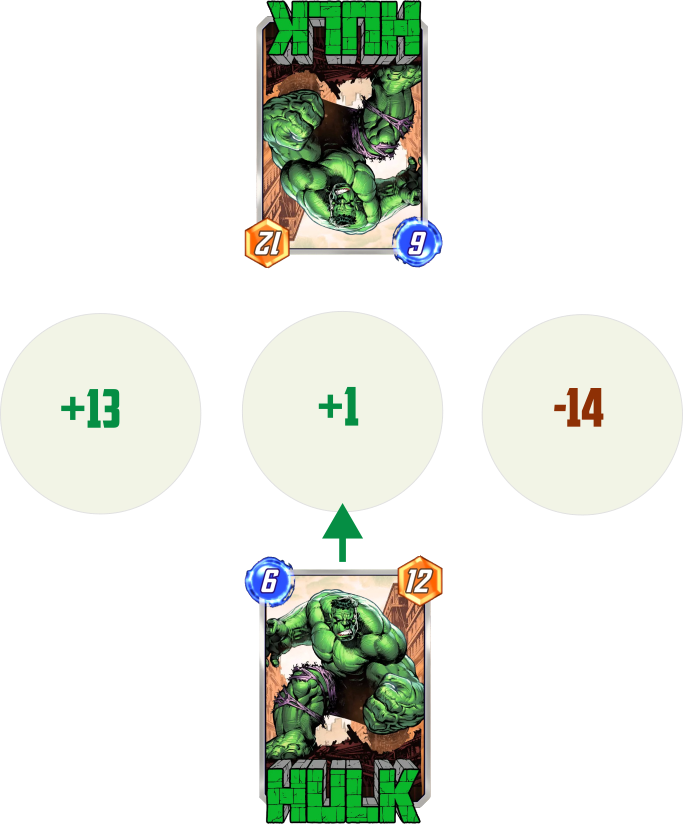
As having a location secured out of opponent’s reach is advantageous, P1 may consider polarizing own investment, so that 1st location gets out of P2 reach, while a minimal lead on the 2nd one is established. P1 would then be able to retrieve 100% winrate again. Such strategy requires overinvestment from opponent on one slot. Note that the final shape of P1 points distribution would be very similar to ‘one-out’ strategy.
To resume, there are two possibly winning strategies for P1 in a duel of chonkers:
- Getting lead on 2 locations while keeping the reach on 3rd (100% wr)
- Getting out of reach on one location, while claiming slight lead on the 2nd (100%)
Chonker vs Split
A ‘Hulk’ last play is analogous to forced investment into ‘mono’ strategy. Being able to play multiple cards into various locations instead gives more flexibility and is overall better. Therefore usually high-end cards must grant some additional effects and benefits over a sum of lower cost tools.
In this study we assume that power = 2*mana cost, so the scaling is linear and split is never worse than a chonker.
The advantage of split over ‘Hulk’ is tremendous. Let’s go back to the simplest chonker vs chonker win scenario, where P1 had more points on every location before the last turn. Even such favorable circumstances may be straight-up game losing against Split, proven that in (+N, +N, +N) state N is lower than the power of 2 provision cost card. Placing 3×2 provision cards then leads to ‘mono’ vs ‘even’ scenario, which is 100% won for P2.
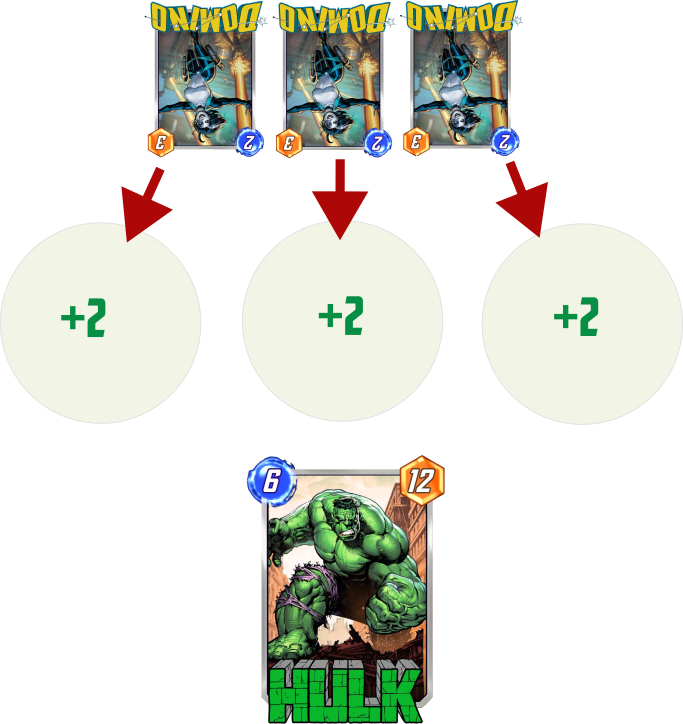
The point lead on multiple locations gives little here, but the reach remains the same as in the duel of chonkers. The only scenario in which chonker wins against split is the second winning strategy of chonker vs chonker – getting out of reach on one location and claiming slight lead on another.
The split player objective is keeping dispersed reach on multiple locations, so that claiming lead on all of them is possible in the last play (neglecting opponent’s reaction). Mimicking opponent’s plays would usually be enough to guarantee the win.
Split vs Split
This matter is complex at the detailed level. If every split is possible, then point differences mean little proven that reach is maintained and same amount of resources was projected by both sides. The outcome then comes down to a 50/50 roll. Overall the situation is very similar to ‘Resource Allocation Game‘.
In practice the splits are usually limited and dependent on used decks. That’s a material for more extensive study.
Closure
In this short article, the concepts of win conditions and point reach in a game of Marvel Snap were demonstrated. We haven’t gone really deep, but nevertheless got some basic insight into how the game is decided in the very last move. Most often the random factor would play a vital role. The only exceptions is assymetry of resources (for example in a favored matchup and/or blessed location RNG), where prefered side could conveniently realize one of winning scenarios described in the article.
Stay tuned!

