Introduction
With Marvel Snap card game getting oficially released on Android, iOS and in early access on Steam, the snapping fashion have come to Gwent community. No wonder I tried the game myself and got thoroughly addicted for two weeks, climbing to infinity with Pool 1 and Pool 2 decks in the last and current season (Symbiote Invasion, Warriors of Wakanda). This article though wouldn’t be the game review or any kind of tutorial.
We would play a different, elementary level game based on resource allocation.
Three Slots Resource Allocation Game
- 2 players
- three slots (locations)
- same number of resources (money bags) for both players
- both players simultanously place resources onto slots, out of opponent’s sight – only one turn
- the player with more resources placed on the slot wins this slot; in the case of same investment, the result on a slot is a tie
- winning on at least one slot more than opponent means winning the game

Basic Observations
Three slots is the lowest number possible for the game to be non-trivial. In the case of only 2 slots, it could be easily seen that every strategy leads to the same outcome – a tied game. Also +1 slot (4 total) is not a good idea assuming current rules – too many games would end in 2-2 draws.
Consequently, 3 slots is a perfect model for the most elementary ‘game theory’ studies. Let me know if you came across comprehensive studies in this matter.
We know that 2-slots game is drawn everytime. How about 3-slots, what conditions lead to a draw? If the amount of allocated resources from both players is different on each slot then the game obviously has to be decisive. Only 2-1 type of the score is possible; 3-0 would require one side to have more resources on each slot and consequently more resources in total.
If both players placed same amount on a certain slot, then given this knowledge, the game on two remaining slots becomes no different to 2-slots allocation. It implies that tie on a single slot leads to a total tie in a 3-slot game with equal resources.
When choosing points distribution on slots, there are two main aspects. The first one is the overall strategy (shape) of the distribution. Would you bank all money on one slot, or maybe distribute it evenly between 1-3 fields? When the shape is decided, the decision where exactly to place which amount has to be taken. The impact of this decision is completely random (let’s call it a roll). Rolls are not really interesting from mathematical/strategical point of view. One could even imagine tuning game rules in such a way that players must fill 1-3 and 1′-3′ in the order from highest to lowest investment. After such modification the impact of rolls vanishes.
Let’s call the amounts set by the shape as bars. There is 3! rolls possible for each player if all bars are different (permutations); 3 if there is a pair of same value bars. The spatial position and ordering though is irrelevant by itself. What really matters is which bar of player 1 (P1) stands against which bar of player 2 (P2). This way each ‘battle‘ and finally ‘war‘ result is decided.
Mathematically, the problem is essentially the same, but instead of vanilla slot numbers, we denote them by ordered indexes of opponent’s bars. There are 6 mutual configurations possible in the usual case, 3 if there is a single pair in P1 or P2 shape, 2 if both sides have a pair.
Basic Strategies - Point Spread Modes
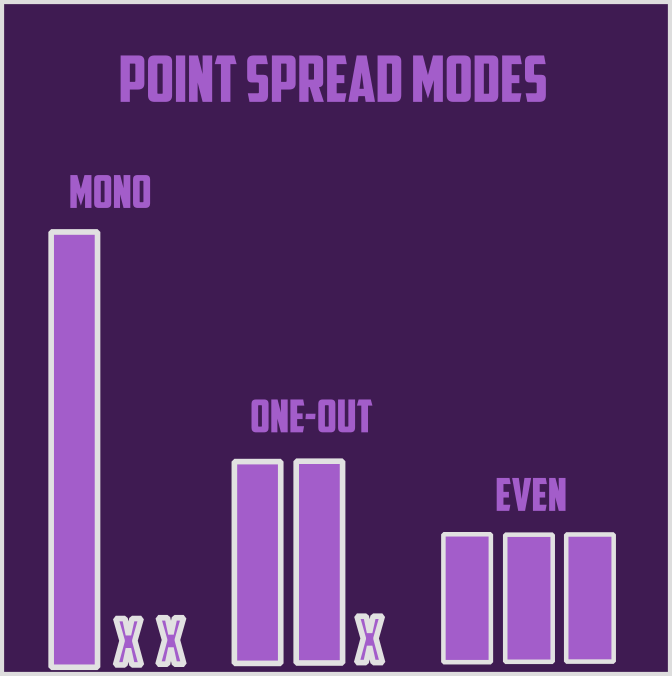
(where ‘X’ stands for an empty slot). In the picture above three basic allocation modes are shown. Let’s analyse them one by one.
- ‘Mono’
All resources are invested in one slot. As the game objective is to win on two slots, this spread obviously is very suboptimal; in fact it never wins a game.
- ‘One-Out’
The most natural approach to achieve a win on two slots is to invest all resources into two nodes and completely neglect the third one. Such strategy is favored against other basic modes; against ‘Mono’ it has 1/3 chance to win, and against ‘Even’ it wins everytime.
- ‘Even’
In ‘Even’ mode, all slots are equally filled. The shape is not polarized to fight for distinguished two locations. ‘Even’ always loses to ‘One-Out’ and always beats ‘Mono’
Judging from the short analysis above, ‘One Out’ is the most optimal basic strategy. By combining presented modes in various proportion, we could retrieve every possible shape and consequently build more complex strategies. It is especially tempting to contest ‘One-Out’ this way.
Complex Strategies - Mixed Modes
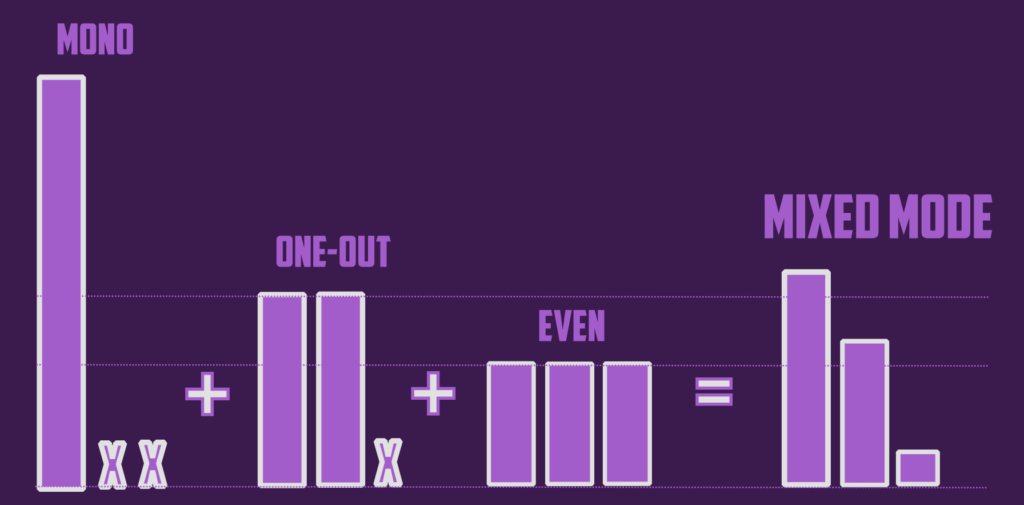
- Basic Killer
Could a mixed-mode shape become favored against every basic spread? Let’s think about it starting from ‘One-Out’. No combination of ‘One-Out’ with ‘Mono’ could help, neither a combination of ‘One-Out’ with ‘Even’.
The third slot without resources is the weak link of the ‘One-Out’ strategy, which lets opponent to win a slot with just minimal investment. A secondary weakness is that just by investing more than half of resources into a single slot, a win on this slot is fully guaranteed. To beat ‘One-Out’:
– One bar higher than 1/2
– Lowest bar non-zero
Such ‘Mixed’ spread beats ‘One-Out’ whenever ‘O-O’ lowest bar meets the lowest or secondary ‘M’ bar, which is 66% of time. Thanks to rolls, a more favored matchup is impossible against ‘O-O’.
The two conditions written above are not enough to beat ‘Even’ at the same time. The task there though is really simple. To beat ‘Even’:
– Two highest bars greater than 1/3
Such ‘Mixed’ keeps 100% winrate against ‘Even’. To achieve ultimate ‘Basic Killer’ we have to combine all conditions. Let’s denote highest bar by A, secondary by B and ternary by C. Then:
A > 1/2
B > 1/3
C = 1 – A – B < 1/6
The lowest bar is never higher than 1/6. Dotted lines in the picture are indicating 1/2 and 1/3 crucial values.
'Basic Killer' In Practice
As long as living in the world of percents and fractions, the space of ‘basic killers’ gives limited, but infinite possibilities. When moving to the discrete world of points or money bags though, the situation becomes more complex. Out of numbers divisible by 2 and 3, the first instance of ‘money bags’ for which ‘Basic Killer’ emerges is 18 units. Then, there is only one single spread satisfying all necessary conditions: 10-7-1. The matchups are illustrated in pictures below.


Concluding Remarks
Obviously, Three-Slots Game is of Rock-Paper-Scissors type, with strategies countering each other to some extent, losing to one shape (not to mention roll) and winning against another. As have been shown though, there are overall worse (‘Mono’, ‘Even’) and better (‘One-out’ and ‘Basic Killer’) strategies. ‘BK’ shouldn’t by no means be viewed as the best, ultimate strategy; it just counters basic, schematic modes in the best possible way. The topic of the best strategy would be investigated soon more strictly with the use of some numerical calculations.
Also, I believe the article invites playing the T-S game itself, trying presented strategies to get edge against non-prepared friend or stranger. The game is a mix of basic math and behavioral psychology – knowing what strategies are chosen most often when playing the game for the first time is the decisive factor. Great field for an intersting machine learning experiment, where strategies chosen by AI depend on past Human players habits. Please let me know if you came across anything worthy in this topic.
Stay tuned!

