Introduction
In this article we would look into Bo3 (best-of-three) conquest format. We would start from the simplest setting. Bans are already done. Only playthrough is left, and all matchups are parametrized with invariant winning probabilities. Coinflip (i.e. who goes first/second each game) is neglected.
While simplest possible, there are some surprises and impactful results in this system, so let’s dive into the analysis.
Defintions and Parameters
Best of 3 conquest is a duel of two players. We will choose first-person perspective here. My decks are denoted by letters in caps: \(A\),\(B\). Opponent’s decks are lowercase: \(a\), \(b\). \(P_{Xy}\) is the probability of deck \(X\) winning over \(y\) in a game. Draws are excluded.
We are interested solely in the competitive aspect at this point, which means we want to maximize \(P_{win}\) = probability to win in a Bo3 match. Bo3 is not an autobattler and we have some queueing freedom.
We have to introduce some strategy parameters: probabilities of queueing a deck at a given stage of the match. Possible deck choice depends on what decks already won and are blocked.
Consequently, it is convenient to use blocked decks as the current state (node) description – the order in which decks were played and past matchups don’t matter at all for \(P_{win}\).
We define \(W\_node\_n\) in caps as our startegic parameters, where \(n\) denotes the probability of choosing n-th deck from the left ones. Similar parameters, but lowercase are defined for opponent.
How many parameters are there then if we add everything up? Notice that W_0_1, where 0 is the starting node is equal to 1-W_0_2. One parameter is enough to describe both probs. Consequently we get:
- \(P_{Aa}\), \(P_{Ab}\), \(P_{Ba}\), \(P_{Bb}\) => matchups table
- \(W\_0\_1\), \(w\_0\_1\),... => strats table
And here one parameter appears for each side having 2 decks left after game 1. We are focused on \(P_{win}\) though, so we observe that:
Any decision taken after first game does not impact \(P_{win}\) in Bo3, because it possibly only changes the order of the forced matchups.
Finally then, our model consists of 6 parameters.
How skillful Bo3 is?
Let’s start our analysis from the simplest case, where win probabilities in all matchups are equal. In such case queuing obviously doesn’t matter, so we drop W’s as well and end up with single parameter p. This parameter describes chances for us to win in every single game.
Similar situations often arise when meta is balanced and only the skill gap impacts game results. Analyzing this model case we simply check out how skillful Bo3 format is with respect to a single game.
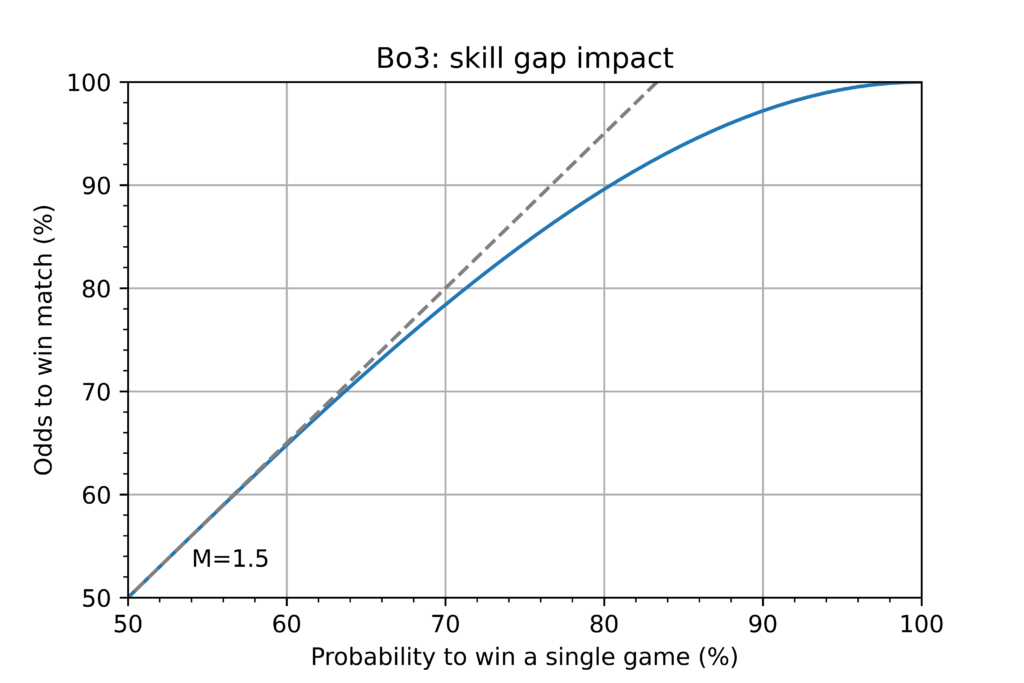
As could be seen, up to ~65% the relation between p and \(P_{win}\) is almost linear. The exact expression for \(P_{win}\) is as follows:
\(P_{win}=-2p^3 + 3p^2\)
If we take derivative with respect to p at p=0.5, then we obtain M=1.5, where M is a skill-Multiplicator. For every 1% edge in a single game there is 1.5% edge in a Bo3.
How important queueing is?
Perhaps the most surprising discovery for me was that…
Due to internal Bo3 system symmetry it is IMPOSSIBLE to get a SYSTEMATIC advantage with proper queueing.
By systematic we mean independent on opponent’s action.
The only way queueing impacts Bo3 is BINARITY
Binarity

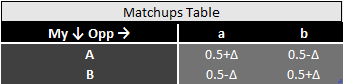
Let’s consider the situation arising when matchup table looks like in the picture above. Let’s say we queue deck A. Opponent may choose a or b.
If a, then we win this game. Only B is left, and matchup against b is certain – match is won.
If b, then opponent wins and is left with a, which always beats B – match is lost.
Analogously for choosing B first, there is one 100% winning and one 100% losing scenario.
There is no better or worse decision to be made a’priori by both sides. However, a’posteriori one decision is winning and one is losing. Match result is simply a coinflip, but unlike a full 50/50 matchups table, everything is decided after first queuing.
This is the exact essence of binarity. The matchup table shown above is an extremal case, but every other possible set of probabilities works in the same way. There are only more and less binary systems – ones where decision strongly determines the future, and ones where it doesn’t matter at all. Objectively good/bad decision systems do not exist! Let’s see how binarity (difference in \(P_{win}\) between two scenarios) changes when we go from 0.5 matrix to the full binary table step by step.
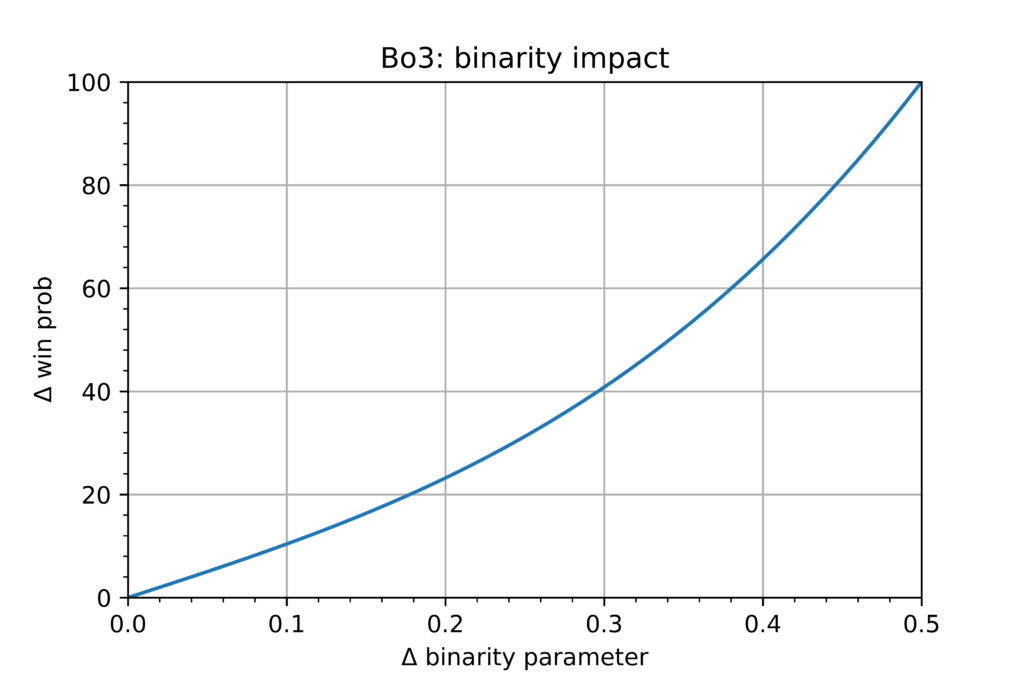
Binarity is equal to zero whenever cross matchups (A-b, B-a; A-a, B-b) sum up to 1! Also important tip: don’t develop constant queueing habits when playing tournaments (for example going always with one deck first) – if opponent is able to read your mind it could give them significant advantage thanks to binarity!
Lineup improvement modes - phasing
There are 4 main modes of improving lineup. The first one was shown in ‘How skillful Bo3 is?’ section. It is all-around improvement, also called ‘git gud at the game’.
The remaining 3 modes (which combined with 1 could construct any other mode as a linear superposition) rely on improving just a pair of matchups. Which approach do you think would be most effective when we start from 0.5 matrix (or maybe it doesn’t matter at all)?
a) Improving both matchups of one deck? (deckwise)
b) Improving different matchups of two decks? (anti-phase)
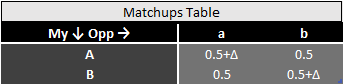
c) Improving same matchup of two decks? (targetting)
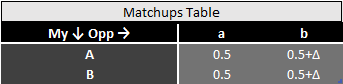
And here is the answer:
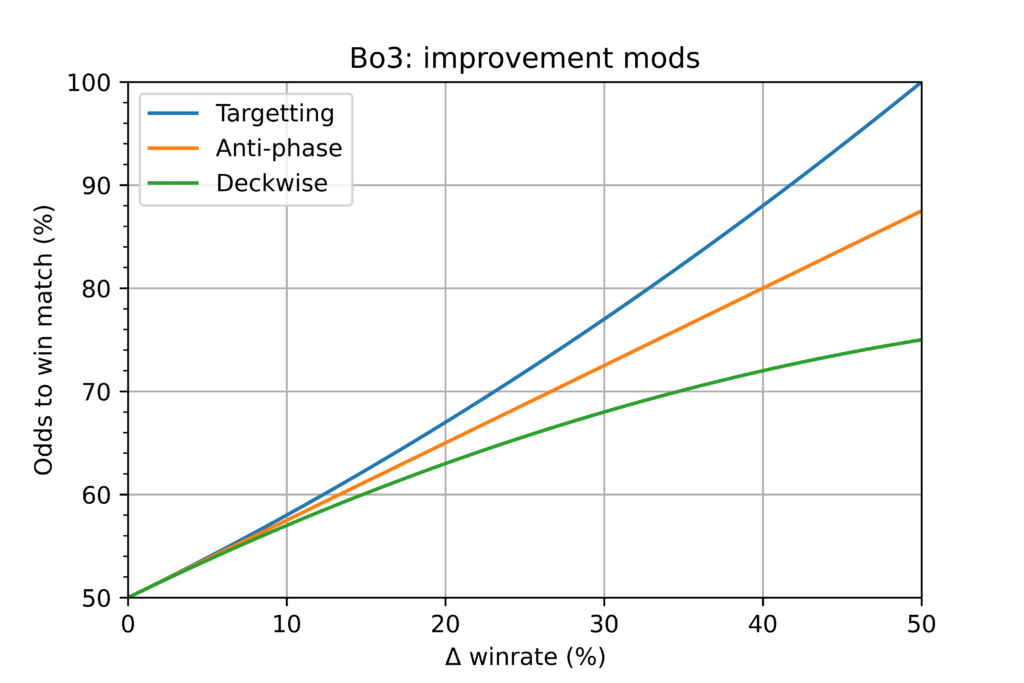
Modes differ and targetting is the most efficient improvement strategy. At the same time it is worth noticing, that the difference between modes is very small whenever improvement is only slight.
Hardcore targetting snowballs and could be very threatening strategy (Lifecoach vs TailBot in Masters 1 Quarterfinals is a classical example)
Anti-phase mode scales just linearly and also leads straight to binarity.
Finally, deckwise optimization scales in the weakest way. Together with Targetting it is a demonstration of fundamental law of conquest format:
A single deck would never win you a match, but easily could lose you a match.
Conquest is a team game between lineups and all decks should work in-phase above all.
Deck Quality and Spreadsheet
How good then is a deck in a Bo3 lineup? There are many ways of assessment. In the attached spreasheet I used following approach:
Rel Quality(X) = P_win (with deck X in lineup) – P_win (with 0.5/0.5 deck instead of X)
Another observation: as there is no systematic advantage possible thanks to queuing, using random queuing (all W’s equal to 0.5) is most convenient for P_win analysis. Therefore Win(random) is the main, highlighted area in the spreadsheet.
Spreadsheet link here (Google Sheet)
Closure
Thanks for reading! Conquest format math is far from trivial and we didn’t even cross game theory mark yet. More about Conquest to come in the future, but rather not too soon.
See you in Bo3!

