Introduction
Nilfgaard popularity is a Gwent phenomenon, confirmed many times in statistical data. If you look for example into GwentData tables, Nilfgaard is the most popular faction in Top500 of Pro Ladder since the Season of the Magic Masters 3. It’s lead reaches 5% advantage over second faction when strong (like in the current data for the Season of the Wolf) or few per mille when weak.
At the same time in all these 8 consecutive seasons of playrate supremacy Nilfgaard was never the best %wr faction. More to it: even placing in Top2 didn’t happen (in Top500 Pro Ladder sample)! At the same time, Nilfgaard was often a faction with a handful of best peak MMR scores amongst top players (Draconid, Dryad).
Is it only an accident and Mill/Cahir/Vattier player preying on Nilfgaard stats, or maybe there is something deeper to it? It appears Nilfgaardian Mages use some refined illusion techniques to make NG perceived as weaker than it really is.
Faction Winrates and Statistical Ensemble
Instead of starting from mathematical derivation, let’s rather just use imagination. We live in a world where Reddit is right. Masquerade Ball is an ultimate broken card, winning every game for Nilfgaard.
In addition to this, Reddit is even more right – Gwent players are filthy, brainless netdeckers and 50% of playerbase goes for NG. What would be NG winrate on ladder?
100% of games against other factions would be won… but there would also be a decent percentage of mirrors. So roughly 50% of games is effectively won for NG and 50% (mirrors) is 50% won. Consequently, absolutely broken faction, the ulimate ladder menace, becomes just nothing more than a 75% winrate faction in general ladder stats.
What we learn from this example is that matchups matter and statistics for whole Pro Ladder have some constraints which are not present for individual players.
Is NG winrate in the thought experiment above exactly equal to 75%? Not really. Imagine now that NG (50%) every time gets paired with other faction (50%). It is highly unlikely, but possible. Then observed winrate is indeed 100%.
Conversely, NG could be matched only with itself – 50% winrate. There is some freedom space and for exact statistics each matchup in each game would have to be known (inaccessible in Gwent 10.1).
In Gwent reality we would suspect that the fraction of mirrors would be higher than 50% (because of all NG grouping on top fMMRs) and consequently faction winrate even lower than 70%. But let’s move on.
Mirror Correction (math)
As we can see, only winrates against other factions are relevant and mirrors are distorting the picture. We would like to obtain the winrate against different factions, while still using general ladder data.
Let’s start from the measured winrate definition (all quantities here relate to a single faction):
\[\%wr = \frac{w}{N}\]
,where \(\%wr\) is faction winrate, \(w\) is the number of wins and \(N\) is the number of games. Now we would split \(w\) and \(N\) into mirrors(m) and other faction (o) contributions:
\[\%wr = \frac{w_m + w_o}{N_m + N_o}\]
Here we observe that \(w_m\) = \(\frac{N_m}{2}\). Let’s define the seeked winrate as:
\[\%wr_o = \frac{w_o}{N_o}\]
Then \(w_o\) becomes \(%wr_{o}{N_o}\). Now some assumptions have to made. We would assume uniform matchups distribution (random matchmaking). It leads to
\[N_m = \frac{N}{N_{tot}}*N\]
\[N_o = (1-\frac{N}{N_{tot}})*N\]
, where N_{tot} is the total number of games played. The denominator in the main equation was decoupled for demo only – let’s substitute N back instead. After all substitutions we get:
\[\%wr = \frac{\%wr_o*(1-\frac{N}{N_{tot}})*N+ \frac{N}{N_{tot}}*\frac{N}{2}}{N}\]
, where N obviously crosses out and we get:
\[\%wr = \%wr_o*(1-\frac{N}{N_{tot}})+ \frac{N}{2N_{tot}}\]
and after moving terms from right to left we get:
\[\%wr_o = \frac{\%wr – \frac{N}{2N_{tot}}}{1-\frac{N}{N_{tot}}}\]
That’s our final expression. We could make it a bit smoother and easier to work with by noticing that playrate \(\%pr\) is just \(N\) to \(N_{tot}\) ratio.
\[\%wr_o = \frac{\%wr – \frac{\%pr}{2}}{1-\%pr}\]
The equation is simple and we need nothing more than \(\%wr\) and \(\%pr\) casually available on GwentData to perform mirror correction refinement.
Dismantling The Nilfgaardian Illusion
One disclaimer before moving on – the math presented here is nothing new – mirror corrected results are most often not published simply because it relies on additional assumptions and takes additional space in the report (I haven’t done it myself ;-))
We could now proceed to dismantle NG illusions one by one. Let’s start from our imaginary example and substitute some numbers:
\[\%wr_o = \frac{0.75 – \frac{0.5}{2}}{1-0.5} = 1 \]
Completely debunked! Now let’s see some real data examples:
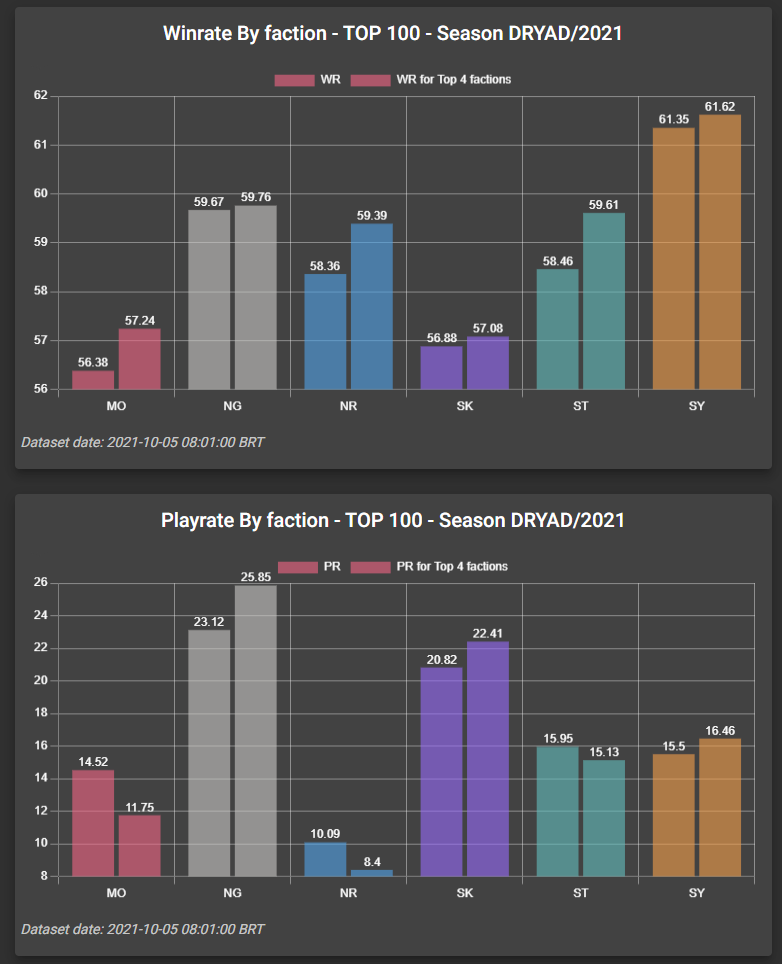
Above are the final results in the Season of the Dryad in Masters 3. Would NG or SY have higher winrate if we apply mirror correction?
NG almost catched up, but SY remains best with ~0.8% advantage. Mirror correction improved NG winrate by ~3%!
Now let’s experiment on some current season data which I gathered.
Have a look how Nilfgaard moves from 3rd or 4th position to Top2 after mirror corrrection is applied! (_picked_winrate => _winrate_corr). We dismantled Nilfgaardian winrate camouflage scheme and their real power appeared!
Closure
Hope that you enjoyed the lecture! See you in Gwent!

