Introduction
Thinning is a card game mechanic revolving around removing unnecessary cards from the deck during the game (thinning the deck). Thinning is supposed to increase the chance of finding crucial cards and combos, making the gameplan more consistent and improving average hand power at the later stages of the game.
Considering Gwent, it is worth noting that Thinning brings benefits only before Round 3 (unless you are able to scroll through your deck in R3).
In this article we would enumerate and present various types of thinning occuring in Gwent. Then we would dive into basic maths of two common thinning modes: reduction and drawing. We would also assess power of a few thinning cards.
Types Of Thinning In Gwent
There are various mechanics in Gwent which could be gathered under collective thinning term, starting from classical (removing card from the deck) up to manipulation thinning (placing card at the bottom etc.). Let’s catalogue these mechanics one by one:
- Tutorial Thinning
Every time a card from hand (a tutor) is used to play a card from inside the deck (tutored card), the deck thins by 1.
+ Normal Tutors
Cards like Royal Decree, Call of the Forest etc. Usually dedicated to pull out missing cards in Round 3. Almost never played for thinning purpose.
+ Echo Tutors
A class of thinning tutors deserving special treatment are Echo tutors (Amphibious Assault, Blood Eagle, Oneiromancy). When played first time, those tutors do not thin deck in a quantitive sense (but could still effectively thin deck out of unwanted cards). Second play though is already normal tutorial thinning
+ Bronze Enhancing Tutors
Some tutors in Gwent are devised to gain extra value from pulling out bronze cards from the deck. Such tutors are usually used in Round 1 to thin out bronzes from the deck. Examples include Amphibious Assault or Novigradian Justice
This definition though is also obeyed by some cards usually played at the later stage, like Mammuna or Simlas.
+ Summoning combo
Another case of tutorial thinning occurs when a played card summons a specific one from the deck. Example is Old Speartip + Old Speartip: Asleep combo.
- Thinning Pairs
There are at least 2 bronze cards in each faction tutoring its counterpart from the deck. The difference with respect to Tutorial Thinning is that no card is distinguished as tutor/target in the pair. In Gwent 10.2 we have following thinning pairs:
Monsters: Wild Hunt Riders, Archespore
Nilfgaard: Impera Brigade, Hunting Pack
Northern Realms: Dun Banners, Blue Stripes Commandos
Skellige: Crow Messengers, Drummond Shieldmaiden
Scoia’tael: Brokilon Sentinel, Mahakam Volunteers
Syndicate: Sewer Raiders, Casino Bouncers
- Draw-a-card
Whenever an extra card is drawn during the round, the deck effectively gets thinned by 1. The simplest examples of draw-a-card thinning tools are Imlerith, Sunset Wanderers or Raffard’s Vengeance.
+ Discard Package
While disguised, Discard package in Skellige works in ‘draw-a-card’ manner. Heymaey Skald played on Tuirseach Skirmisher is equivalent to Imlerith discarding 5 power 4 provision card.
The thinning comes from Skalds, Birna, Coral, not from Morkvarg and Skirmishers.
- Pull-out thinning
When it comes to raw mechanics, Pull-out thinning works in similar way as tutor thinning, but there is a random factor governing which exact cards would be thinned (in general case). Examples of pull-out thinning agents are Saskia: Commander, Portal or Iorveth’s Gambit.
- Self-thinning
Some cards could thin out of the deck by themselves. Examples include Roach or Knickers. Similarily Cerys:Fearless, The Flying Redanian, King of Beggars and Madoc self-thins when certain conditions get satisfied.
- Erasing
Cards like Derran or Dead Man’s Tongue are capable of removing unwanted cards from the deck without playing them.
- Milling
By discarding and banishing cards from opponent’s deck, it effectively gets thinned, but most often without or with negative benefits.
- Manipulation thinning
It is debatable if own deck manipulation should be called ‘thinning’ as it doesn’t involve physical reduction of number of cards in the deck. Still merits are similar. Cards like Jan Calveit or Maxii van Dekkar belong here
- Complex thinning
Complex thinning consists of more than one thinning effect or unique abilities. Examples include Eavesdrop and Emhyr var Emreis.
- Negative thinning
Negative thinning happens when cards are added into deck body instead of being thinned out. Examples include playing against Cloggers, cards like Yennefer’s Invocation etc.
- Leader thinning
In Gwent 10.2 there are four leaders capable of thinning your deck:
+ Precision Strike – thinning by 2 if Brokilon Sentinels are in the deck
+ Blaze of Glory – thinning by 1 by discarding a card from the deck
+ Imperial Formation – could thin the deck by 1 if likes of Mage Assassin/Affan Hillegrand are present in the deck
+ Tactical Decision – could thin out Assassins/Affan present in hand or drawn after using leader ability.
Leader thinning is specific, because it is guaranteed during the game and always means power commitment when used.
- Stratagem thinning
In Gwent 10.2 there are two stratagems capable of thinning:
+ Cursed Scroll – thins the deck in the manipulation way by placing one card from hand at the bottom
+ Mask of Uroboros – classical ‘draw-a-card’ thinning combined with discard of one card from hand
Two Main Thinning Modes
While a rich catalogue of thinning opportunities was presented above, there are in fact two main thinning modes present in Gwent:
- Reduction Thinning (tutorial, pairs, self-, erasing, pull-off…)
- Drawing Thinning (draw-a-card)
Reduction Thinning
We thin one card from the deck from a random slot. As we’ve shown in GM&P2, as long as the deck could be treated as a blackbox, hypergeometric probabilities would work perfectly fine to estimate the chances of drawing cards.
Card pool then gets reduced from 15 to 14 cards during R2 mulligans and from 12 to 11 during R3. In the section 4. of GM&P2 we have an example of how simply calculate the chances of finding a single card. Let’s remind:
chance to find= 1 – chance to miss the card completely = 1-(chance to miss R1)*(chance to miss R2)…
, substituting for both coins:
Red: 1-(1-12/25)*(1-5/14)*(1-5/11) = 81.77% (+2.0%)
Blue: 1-(1-13/25)*(1-5/14)*(1-5/11) = 83.17% (+1.8%)
,where values in () denote change with respect to no thinning. A thinning pair definitely would not help a lot if your deck relies on drawing a single card!

The odds to find a single card grow in a non-linear manner; 2nd thinning is worth more than 1st, 3rd more than 2nd and so on. Still it doesn’t snowball fast enough to replace a single tutor (~97% chance to find a given card) as an insurance in any combo deck.
After 7 cards are thinned out, all cards in the deck are accessible! It is easy to see as without thinning there are 12 cards left in the deck before R3 mulligan. If 7 cards got thinned after R1, then in R3 only 5 cards are left and obviously all of these could be accessed during mulligan phase.
As we observed, thinning is a measure to improve overall hand quality rather than to find a single card. How about drawing a set of cards then? Let’s say that our exemplary deck plays 10 golds (or just 10 cards best for a long R3 in a given matchup with duplicates neglected). How would the average number of golds drawn improve thanks to successful thinning? (cheatsheet with all tables from this article in Google Sheets).
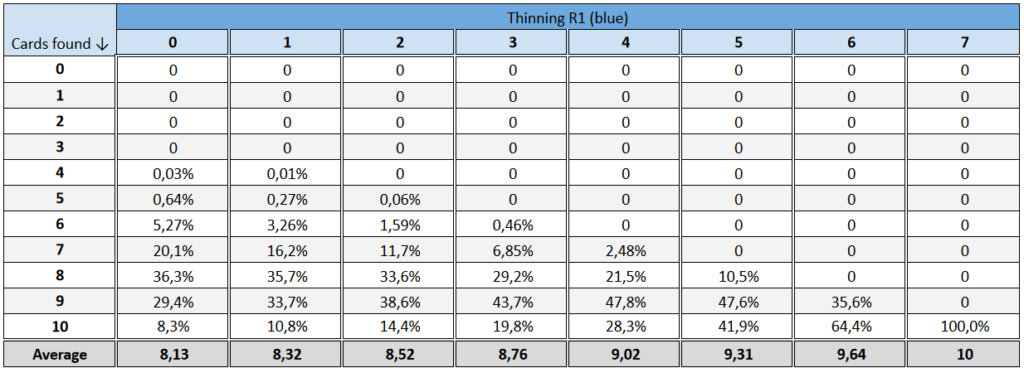

As could be seen by comparing graphs, the % of crucial cards drawn is exactly equal to % chance to find a single card.
The distribution of possible # of cards drawn becomes more and more tight with the increase of R1 thinning.
What could be surprising is that even after thinning 6 cards after R1, the chance to miss one of Top10 R3 cards is considerable (35.6%/38.5% or blue/red). In other words, almost 4/10 times R3 hand is not perfect. It seems awkward and unjust. Let’s look into the underlying mechanism more.
As said earlier, the deck is a blackbox – nothing is known about card sequence. With 6 cards thinned out after R1, exactly 1 card wouldn’t be drawn after R3 mulligan (6 cards left in the deck). What is the chance this card is one of 10 golds?
After R1 cards are thinned out at random. In order to miss a gold:
- It has to be at the bottom after R1
- None of cards mulliganed out after R2 could land below
Important thing, which is easy to overlook: the card doesn’t have to be at the bottom at the very start! That’s because cards could be thinned not only from above, but also from below a given slot (remember thinning paradox?).
- Let’s say we are on red coin. (12/25) = 48% of golds are found in R1 on average, which means that 52% remains in the deck. There are 15 cards outside hand, but 6 cards would be thinned out from random slots. The cards thinned out are obviously not the cards we want to find. Therefore after thinning there would be 5.2/9 = 57.77(7)% chance that the last card is gold.
- Two cards would be mulliganed out be default after R2. Let’s imagine that cards go back to deck one after another. The chance that the first one lands above is 4/5; the second one: 5/6. Both events has to happen, so the chance that the card remains at the bottom is equal to 4/5*5/6= 2/3
Multiplying the probability of both events we get P(miss a gold) = 0.385…, which is equal to the value displayed in the table.
Drawing Thinning
Draw-a-card thinning operates by drawing a card from the top of the deck. While normal reduction thinning removes the card from a random slot in the deck, ‘draw-a-card’ thinning is combined with scrolling and thinned cards never come from the bottom of the deck.
In the mathematical sense, another card drawing phase is added (‘draw one card from the deck’ for Heymaey Skald, draw 2 cards for Birna…) and the deck is thinned after each such phase.
Let’s start from the simplest calculation of drawing a single card when using a single ‘draw-a-card’ thinning in R1. It appears that we could simply use old expressions (with single thinning R1), where the subtracted product is multiplied additionally by the chance to not draw the desired card from the top (=14/15)
Red: 1-(1-12/25)*(14/15)*(1-5/14)*(1-5/11) = 82.98% (+3.2%)
Blue: 1-(1-13/25)* (14/15)*(1-5/14)*(1-5/11) = 84.29% (+3.0%)
The improvement of card finding chances is visibly better than in the case of reduction thinning. For the sake of simplicity, we would here also restrict ourselves to R1 thinning only.

Comparison with Reduction thinning:

As could be infered by analogy, with thinning 6, the 10th card from the perfect hand would be missed in 22% of cases. It gives almost 15% improvement with respect to Reduction thinning, but still may be a bit disappointing.
Thinning Cards Evaluation
The ideal R1 thinning scenario describes the ceiling of the value which should be added to the raw points because crucial cards are easier to find.
Obviously, to make any generalization here we have to introduce loads of new assumptions. Let’s say there is no duplicates amongst Top10 cards for R3, and the average difference in power between one of these and non-Top10 is equal to Δpow. Let’s define the difference in the average number of Top10 cards found between +1 R1 thinning and no additional thinning as Δfound . Then the ‘carryover’ value VT of a thinning agent could be estimated as:
VT = Δfound* Δpow
The higher the discrepancy in power between Top10 cards and the bulk is, the more important thinning becomes. To compute some numbers for demonstration value, let’s say we play a model deck with 10 golds worth 10 provision and 15 bronzes worth 4 provision (cost sums up to 160). Let’s use old power vs provision curve. The difference in power would be ~6 points on average and let’s say the baseline for Δfound is no thinning.
Thinning pairs
Thinning pairs work according to Reduction mode. Therefore Δfound ~0.2 and:
VT =0.2*6 = 1.2
A single thinning pair effectively plays for 1.2 points carryover.
Let’s say that a thinning pair succeeds everytime when found R1 (~76%) and possible R2 use is neglected. It should still be treated rather as best case scenario, as we ignore the probability of
pair not getting triggered for some reason, as well as bricking in the last mulligan.
E[VT]= 1.2*0.76 ~= 1.2*3/4 = 0.9
, where by E[] we simply denote expected value. New simplified view on the thinning pair should be then: power + 1 carryover value. For example let’s look into Wild Hunt Riders. The pair plays as 8 points for 6 provision + 1 carryover. According to Power vs Provsision curve, this total value is slightly below meta level for 6 provision (9.6 points), but card may still see play when Top10 garnish is well defined and playing for carryover is possible (no reason to conquest R1 at all cost, no possibility to improve main matchups in R3 by playing sth else in this slot).
Looking into all thinning pairs it is clear now that all these cards are a bit underpowered by itself but for one exception (Gwent 10.2). Archespore has potential to play as 8 for 4 with +1 thinning carryover, which is good value.
Thinning pairs deserve roughly +1 value buff (+2 would be a bit too much, but refreshing and not troublesome at all either) to be considered at meta level.
Tutorial Thinning (Blightmaker)
Tutorial thinning is distinguished from pair thinning by being one direction:
Tutor => Target
Only drawing tutor enables thinning. In Gwent 10.2 meta perhaps only Blightmaker+Mage Assassin combo could be considered a thinning of this type (although Assassin is not really played from the deck if we are fixed on details).
Instead of 76% (thinning pair) we have 50% to trigger thinning in R1 now. Also when the target is exclusive to be tutored rather than played (as Mage Assassin or Bare-Knuckles Brawler with Novigradian Justice), it could brick. We would neglect this contribution though, as we did with bricked thinning pair.
VT,tutor= 1.2
E[VT,tutor]= 1.2*0.5 = 0.6
One Blightmaker+Assassin thins less consistently than a thinning pair, so we can roughly add +0.6 carryover value to all these cards.
The main difference with respect to thinning pairs is that Blightmaker including carryover (11.6 points) plays +2 above power vs provision curve (9.5 points). The card is very powerful even without the thinning effect; often could be Top10 card in the deck itself.
Draw Thinning (Heymaey Skald)
Heymaey Skald is an example of draw-thinning card. The Discard package requires a deeper analysis (which will probably follow soon in one of the next articles). We would here restrict ourselves only to thinning carryover evaluation.
VT,draw = 0.3*6 = 1.8
And the estimated value in games (50% found in R1):
E[VT,draw]= 0.5*1.8 = 0.9
As we could see, Heymaey Skald plays almost for 2 effective points of carryover when found in R1. On the other hand, the card becomes very bad at later stages. To be discussed in separate article on Discard. Even with 1.8 carryover value, needs Skirmisher/Morkvarg payoff to play above power vs provision curve. When it happens, the card plays for very good value thanks to thinning carryover, almost 10 points.
Self-Thinning (Knickers)
Self-thinning cards jump out of the deck when only (usually easy to fulfil) condition is satisfied. The result of self-thinning is identical with the result of reduction thinning, but more consistent; self-thinning card doesn’t have to be drawn, so we could approximately say it works in 100%. In reality there is some bricking risk.
VT,self = 1.2
E[VT,self ] = 1.2
In practice the carryover value is lower, because self-thinning cards usually cost considerable amount of provision and weaken the set of Top10 cards. This topic also deserves investigation in the future, we won’t dive into more complex analysis here.
Outside the thinning value, it is worth to build proper understanding of what self-thinning card does. Let’s take Knickers for example. He could jump out at a random moment, usually it would happen in R1. He costs 7 provision. Then what we effectively do is playing a +3 value bronze card worth 7 provision, which we always commit in R1. This imaginary card is also guaranteed in hand in R1 and gives VT,self thinning value.
Closure and Takeouts
Thanks for reading! While GM&P cycle is supposed to incentivize own studies and deeper understanding of underlying math in Gwent, here is a summary of important takeouts not needing a deeper analysis:
- Thinning is not obligatory for Gwent decks. You don’t need any thinning to find crucial card 80% of time and with tutor it would be 97%.
- Don’t force thinning in your deck. The net gain from a single card thinned out is not impactful. Play thinning cards only when good by itself.
- There are two main thinning modes in Gwent. Drawing thinning is generally stronger than Reduction thinning.
- Thinning 7 cards out of the deck let’s you find any card.
- Unless thinning perfectly, randomness could not be avoided. There is >35% chance to miss a good card when reduced 6 bad cards from the deck in R1.

