Introduction
Fifa World Cup 2022 tournament is the harvest time for bookmaking companies. No wonder that the advertisment action intensified and many people catched gambling bug. Obviously, Gwent: The Witcher Card Game community proven to be no less prone to gambling addiction than the outer world.
In this article we would look into bookmaking fundamentals from mathematical point of view. Nevertheless, the lecture would not be dry math expressions. Surfing through the internet I found impressively concise and informative pdf presentation in Polish, on which this article would be based. Most of my creative work here would be extensive explanation of main points made in this study.
What Is A Bet?
Bet is a contract between player and bookmaker. Bookmaker picks an event and offers odds for chosen outcomes. Odds are return rate of the bet stake. Player bets on one of outcomes and wins if it occurs. In case of a win, the stake multiplied by odds returns to the player. If player lost, then all stake goes to bookmaker.
In Europe decimal odds are commonly used. For example if player wins a bet with 1.75 odds and 100$ stake, then 1.75*100=175$ returns to them. The net profit is equal to 175 – 100 = 75$.
From mathematical point of view, making a bet means prescribing two values to two outcomes of a random event X:
- \((Odds \times Stake) – Stake \) if X happens
- \(-Stake\) if X doesn’t happen
For the sake of simpler math we would assume a unit stake for the rest of the article. The numbers then would express the fraction of money gained/lost. For example -1 means that all money is lost, while 0.25 means +25% profit.
Expected Value (Profit)
Event \(X\) happens with probability \(P_X\). Consequently, there must be \(1 – P_X\) probability of failure. Let’s denote the odds as \(K\). Expected profit from bet B could be expressed as:
\[E(B) = P_X\times{K_X-1} + (1-P_X)\times{-1}\]
, which simplifies to:
\[E(B) = (P_X\times{K_X}) – 1\]
The expression could easily be verfied by subsituting \(K=2\) and \(P_X=0.5\), which is a classical coinflip bet. E(B) is such case is equal to 0 – exactly as should be expected from a fair bet.
Betting is a zero sum game, or in other words, expected profit of player E(B) is the opposite of bookmaker profit (-E(B)). For bookmaker to achieve profit in the long term, the game must be unfair (E(B)<0). Substituting this condition into E(B) expression, we get following inequality:
\[\frac{1}{K_X} > P_X\]
The reversal of odds is supposed to be at least slightly greater than the real probability of the event for bookmaker to achieve profit
Margin Or Bookmaker's Profit
Bookmakers themselves decide how much to tweak the odds. The objective is to achieve a defined profit M from every bet:
\[M = (P_X\times{K_X}) -1 \]
This profit is called margin. Without complimentary event odds it is impossible to strictly assess margin value. Otherwise, player would have to know the exact model used by bookmaker. For example if there is a bet with 100.0 odds for Cristiano Ronaldo to shoot a hattrick in a football match, we cannot compute margin value, unless odds for CR7 to fail this accomplishment are provided as well.
Luckily matches have complimentary outcomes – if team A wins then team B loses or there is draw. With odds provided for each result, we arrive at a system of linear equations, which resolve both probabilities assessed by bookmaker and margin used. The only assumption is that margin is constant for each (win A/draw/win B) bet. The final expressions are as follows.
- Margin
\[ M = \frac{1}{\sum_{i=1}(1/K_i)} – 1 \] - Probabilities
\[P_i = \frac{1+M}{K_i}\]
Attention: in this convention the margin is viewed from player’s perspective, which means negative value.
Taxation
Gambling winnings could be taxed in various ways. In Poland there is 12% bet games tax paid from every bet won, no matter the stake (there are another ones when the winnings threshold is exceeded). With margins being around 3% level, the tax is a vital factor for legal gamblers in Poland.
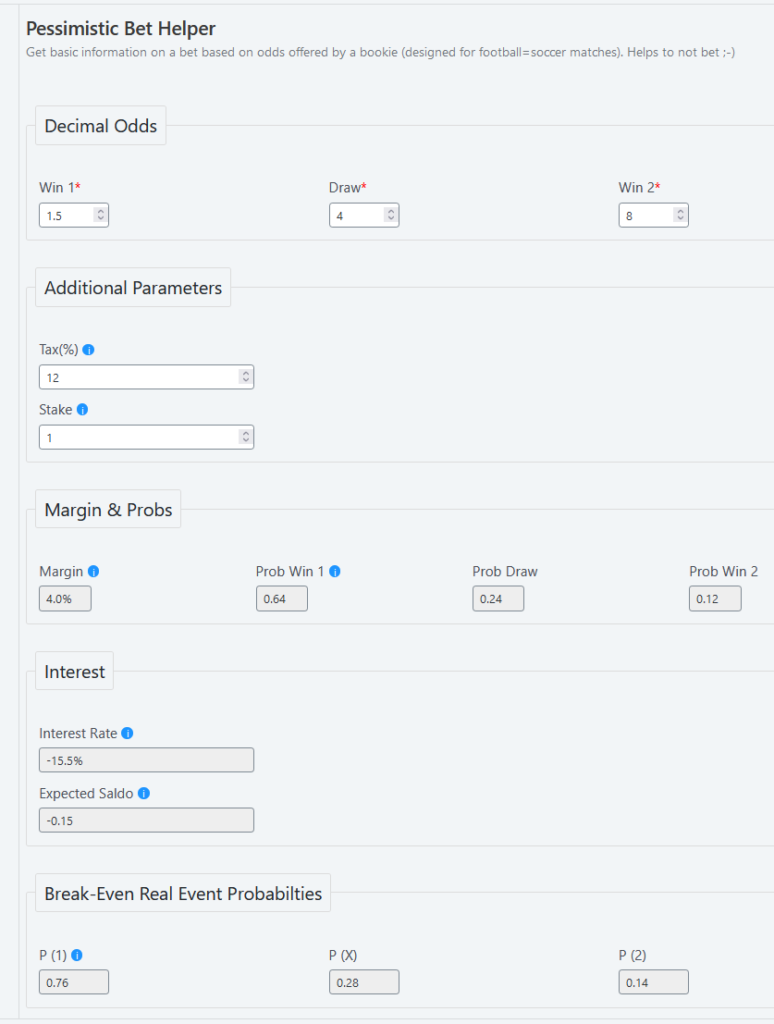
Margin, Probs & Profit Calculator
There is a new, simple calculator provided on leriohub to estimate margin value and other parameters from odds.
The tool is mostly for hands-on demo use. Just type in odds in a match that brought your attention and see how good the offer is. You could also note predicted chances for both teams to win the game or draw.
In Poland, with 12% tax, the interest rate from a normal bet would always be in -15% region.
Betting Basics - Conclusions & Observations
- In its core, bookmaking is a very simple business, where provided odds are the product and manifestation of ‘know-how’. You could scrap odds from any online betting operator and run your own business with good profit (just kidding) 😉
- Bookmaker odds are pretty good indicator of event probabilities, which may be useful outside gambling itself. Remember to aquire them for complimentary events – not just as a reversal of any single outcome odds.
- The margin value couldn’t be too high because of competition with other bookmakers / lower popularity of bets, nor too low, because guaranteed profit is needed in the long run.
- Bookmakers who offer low margins should usually be prefered, but it is also possible to directly compare odds for a single outcome between many bookmakers instead.
- “Safe-bets” do not exist; otherwise bookies would have gone bankrupt very fast.
- Humans have very weak intuition when it comes to exact probabilities compared with statistical analysis. It’s like predicting dice rolls without throwing the dice billions of times.
- The fact that bookmaking business does really well in spite of taxation confirms that gamblers are nothing but rational when it comes to profit. In spite of 12% tax, the business flourish in Poland, with each Ekstraklasa team having a bookmaker sponsor.
- To achieve regular income from bets, player has to estimate probabilities better than bookie, including margin and taxation value.
Could We Beat The Bookmaker Already?
We just learned about margin and expected profit from a single bet. To beat the bookie we have to estimate probabilties better than them. Otherwise we could only minimize average losses by choosing best offers on the market.
Bookmakers use complex statistical analysis systems relying on big data to estimate probabilties. Casual gambler would never have access to similar amount of useful information. Many bookies even provide some stats themselves to customers to let them do analytical job. That’s because its virtually impossible to beat the bookie using a fraction of the same data as them. Thinking that you could beat hundreds of regular job data analysts with decades of experience this way is naive, let alone overcoming the margin + taxation barrier.
The only way to assess probability better is match fixing thinking off the books. Player needs to make the best of human advantages over machine, then use machine and statistics to confirm the findings. For example in a game of Football (Soccer), human knowing the underlying principles of gameplay may find elements overlooked by bookie’s system. For example:
- What is the stake of the match? Are teams going to fight for the win actively or give up?
- How fast are Team A forwards with respect to Team B defenders? How high is Team B defending line supposed to play? – could be especially useful for goalscoring bets
- Is Team A playmaker matched by a good defensive midfield from Team B?…
The hard part is validating the principles on the past data (are the crucial observables accessible?) and without doing it, the method wouldn’t be reliable.
It is practically impossible for casual gambler to beat bookmaker in the long run this way – predicting probabilties better than them is too much effort.
Is bookmaking just a terrible investment for the customer by default then? Well, we lost one battle, but the war is still on. Time to recall the old Sun Tzu proverb: To know your enemy, you must become your enemy.
How Bookmaker Earns Money?
All the principles governing odds and profit would be true if gamblers were rational. Bookmaker doesn’t deal with a single rational customer though, but with thousands of irrational gamblers for the most part. Let’s denote the total money bet on an event by \(S\), and by \(s_1,s_2,…,s_N\) sum of bets on particular outcomes. Then expected bookmaker’s profit \(G\) is equal to:
\[G = S – \sum_{i=1}{s_i\times{P_i}\times{K_i}}\]
A group of model consumers would bet randomly between all outcomes, knowing that no matter the choice, the profit is always negative and equal to M on average. Real people though behave in a different way. They have own behaviors and favorite teams, which added together become global trends. In reality then, probability evaluation of various events is only one half of data work done by bookmaker. The second half is their own customers response to odds, margins and sides involved in a bet.
To maximize \(G\), bookmaker could tune the odds \(K_i\) beyond the \((1+M)/P_i\) value! To hide this action from aware customers view, bookmaker keeps margin constant. The point is to lower the odds for outcomes with high \(s_i\), while better consumers interest at the outcomes with low \(s_i\) is less relevant.
Bookmaker had M income guaranteed, but becomes greedier and tries to maximize profit. Such procedure also reduces possible bankruptcy risk after unlucky streak for a bookie; while big companies could afford temporary losses easily, small bookies may not have enough capital to cover all payouts.
That’s probably also one of the reasons why so many bets are offered by bookies. Spreading the bets over as many events as possible lowers the variance. It is close analogy to investment into multiple stocks.
To keep margin constant, bookmaker simply uses adjusted (fake) probabilities in the odds expression. These probabilties are what a customer resolves when analyzing a bet offer. For example for a 2-ways event (Team A wins/Team B wins), we have:
\[G = S – s_1\times{P_1}\times{\frac{1+M}{P_{A1}}} – (S-s_1)\times{(1-P_1)}\times{\frac{1+M}{(1-P_{A1})}}\]
,where P_{A1} is fake probability of event 1 adjusted to maximize bookmaker’s profit.
Adjusted Probabilities - Example
For simpler arithmetics, let’s assume that bookie estimated probabilities equal to real ones: \(P_{pred}(X) = P(X). The adjusted probability could be expressed then as:
\[P_{Ai} = P_{pred, i} + \Delta_{Ai} = P_i + \Delta_{Ai}\]
The gamblers in our example would belong to two groups. The first one (F) are die-hard fans of Poland national team. They would bet on Poland no matter the odds. There is N% of them. The second group (R) are rational gamblers, betting at random when suggested probabilities are equal to real, and reacting to each adjustment. Bookmaker would suffle \(P_{A1}\) (Poland wins) higher than the real value \( (\Delta_{A1}>0)\) in order to lower the odds and payouts. Let’s assume that (R) react according to logistic function:
\[\begin{cases} \displaystyle
s_1 = \frac{1}{1+10^{W\times{\Delta_{A1}}}}\\
s_2=1-s_1
\end{cases}\]
, where W is a parameter describing how stiff (R) response is. We treat S as unit to reduce the number of variables. Substituting all these to expression for G, we could resolve it for \(\Delta_{A1}\) which grants maximal profit. P(1), N, W and M are model parameters (I have mercy – no symbolic maths here). For example if N=50%, W=10, M=3% and P(X)=0.5:
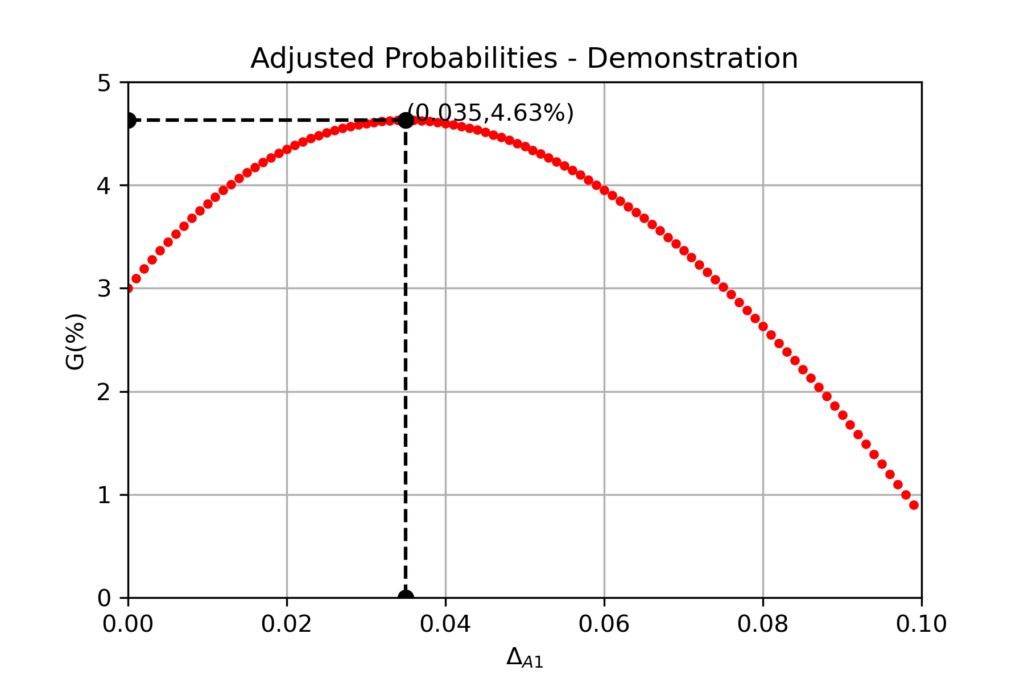
To maximize profit, bookmaker sets the odds using \(P_{1A} = 0.535\) instead of the real event probability \(P1=0.5\). The expected gain over margin is equal to 1.63%.
Instead of 1.94/1.94 (margin 3%), the odds become 1.81/2.08. Betting against Poland, gambler could expect following profit:
\[E[B] = 0.5\times{2.08}-1 = 0.04 = 4\%(!) \]
The net profit of gambler is even higher than bookie’s margin! On the other hand, a die-hard fan of Poland:
\[E[B] = 0.5\times{1.81}-1 = -0.095 = -9.5\%\]
Kurwa.
Greed Is The Main Bookmaker Weakness
Finding the adjusted odds is the main way to win over bookmaker. In other words, we have to trust in bookie’s greed.
Determining which odds are adjusted is not so easy. Note that the presence of competitors severly limits the greed – odds couldn’t be too low.
In order to be serious about playing for profit, gambler has to develop own model after all, which would be able to reproduce bookie’s assessments. Then odds which would vividly differ from model predictions are very likely to be adjusted.
Closure
Time to end the lecture on the fundamentals of bookmaking. Hope I’ve helped you to understand what this game is all about!
This article is by no means an invitation to gambling. Learn to think in a critical way. Remember how we started from hopeless position after basic analysis. Sun Tzu principle: to know your enemy, you must become your enemy teached us to step into opponent’s shoes before deriving final conculsions. These would be made by you, we have to finish right now with a glimpse of hope. Ah, and don’t forget that Bet Calculator is at hands when you need to evaluate a single bet fast!